2006-07-24 ウィスパー3―その4―
ウィスパー3の開発,ようやく終盤戦になってきました。読んでいる人はたぶん一人か二人だと思うので説明がいい加減になってしまいそうですが,はりきっていきましょう。
差の扱いを変更
大掛かりな仕様変更をしました。式の書換えを考えているうちに,どうも現状の仕様ではうまく処理できないことに気づいたのです。
問題は「差」の扱いでした。いままで式が云々という話を散々してきましたが,最終的に何が出力されるのかというと,SQL文が出てくるのです。SQLではそのまんまEXCEPTという演算子が「差」の意味なので,素直に関連付けられると思って何の疑いもなく「差」という演算子を考慮していました。
ところがどうも論理積,論理和,否定で式を処理するのが理に適う気がしてきました。論理演算で差のようなものは,論理積(∩)と否定(¬)で表すことができるはずだからです。そこで「A-B」があったとしたら「A∩¬B」とすることにしました。
書換え規則
論理積(∩),論理和(∪),否定(¬)で表した式をなるべく短くする規則を考えました。以下は書換え規則の一覧です。
| 入力 | 出力 | 備考 |
|---|---|---|
| X∪X | X | R1 |
| X∩X | X | R2 |
| X∪(X∩Y) | X | R3(未実装) |
| X∩(X∪Y) | X | R4(未実装) |
| (X∩Y)∪(X∩Z) | X∩(Y∪Z) | R5(未実装) |
| (X∪Y)∩(X∪Z) | X∪(Y∩Z) | R6(未実装) |
| φ∪X | X | R7 |
| φ∩X | φ | R8 |
| X∪¬X | X | R9 |
| X∩¬X | φ | R10 |
※φは空集合
論理演算の教科書に載っている公式とよく似ています。一部はまったく同じです。おそらく見たことがある人もいると思います。
現在,実装しているのはR1~R2,R7~R10です。R3~R6は実装していません。仕様上,存在するだけです。たぶん出現頻度が低いからです。稼動させてみて頻発するなら実装するつもりです。式の書換えは実行効率をよくするためのものなので,抜けがあっても致命傷にはなりません。
式の書換え
書換え規則を並べてみたところで,これを実際にやるにはちょっとした工夫が必要です。人間の脳みそで考えると「こことここが一緒だから,まとめられる」とか「消せる」と式を見ただけで気づくのですが,現在のコンピュータではそうもいきません。
式は2分木で表しているので,実際にやることは木の枝を切ったりノードを付け替えたりすることです。2分木を使わない方法もありそうですが,思いつきませんでした。
最初に照合元のノード(書換え規則の一覧でいう変数X)を選びます。つぎにX以外のノードについて,おのおの書換え規則と一致するか照合していきます。一致するノードを見つけたら書換え規則に沿って木を書き換えます。
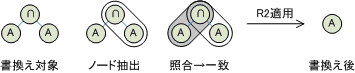
<画像の説明>R2の適用例です。例にしては簡単すぎるのですが,図がないとさっぱり意味が分からないのでつけました。
問題はパターン照合の手間です。今回は「式の長さは最大15項」という制限があるので,木はそれほど大きくなりません。実用的な速さで解けるのですが,どうも小奇麗じゃない気がします。本当にこれで良いのかというと腑に落ちないところがあります。